Em uma distribuição normal, os dados são simetricamente distribuídos sem inclinação. Quando plotados em um gráfico, os dados seguem uma forma de sino, com a maioria dos valores agrupados em torno de uma região central e afunilando-se à medida que se afastam do centro.
Distribuições normais também são chamadas de distribuições Gaussianas ou curvas de sino por causa de sua forma.

- Por que as distribuições normais são importantes?
- Quais são as propriedades das distribuições normais?
- Qual é a sua pontuação de plágio?
- Regra empírica
- Teorema do limite central
- Fórmula da curva normal
- Qual é a distribuição normal padrão?
- Probabilidade usando a distribuição z
- Perguntas frequentes sobre distribuições normais
Por que as distribuições normais são importantes?
Todos os tipos de variáveis em ciências naturais e sociais são distribuídas normalmente ou aproximadamente normalmente. Altura, peso ao nascer, capacidade de leitura, satisfação profissional, ou pontuação no SAT são apenas alguns exemplos de tais variáveis.
Porque variáveis distribuídas normalmente são tão comuns, muitos testes estatísticos são projetados para populações distribuídas normalmente.
O entendimento das propriedades das distribuições normais significa que você pode usar estatísticas inferenciais para comparar diferentes grupos e fazer estimativas sobre populações usando amostras.
Quais são as propriedades das distribuições normais?
As distribuições normais têm características chave que são fáceis de identificar nos gráficos:
- A média, a mediana e o modo são exatamente os mesmos.
- A distribuição é simétrica em relação à média – metade dos valores ficam abaixo da média e metade acima da média.
- A distribuição pode ser descrita por dois valores: a média e o desvio padrão.


A média é o parâmetro de localização enquanto o desvio padrão é o parâmetro de escala.
A média determina onde o pico da curva está centrado. Aumentando a média move a curva para a direita, enquanto que diminuindo ela move a curva para a esquerda.


O desvio padrão estica ou aperta a curva. Um pequeno desvio padrão resulta em uma curva estreita, enquanto um grande desvio padrão leva a uma curva larga.


Regra empírica
A regra empírica, ou o 68-95-99.7 regra, diz-lhe onde se encontra a maioria dos seus valores numa distribuição normal:
- Around 68% dos valores estão dentro de 1 desvio padrão da média.
- Around 95% dos valores estão dentro de 2 desvios padrão da média.
- Around 99,7% dos valores estão dentro de 3 desvios padrão da média.
Seguir a regra empírica:
- A média de 68% das pontuações está entre 1000 e 1300, 1 desvio padrão acima e abaixo da média.
- Terra 95% das pontuações estão entre 850 e 1450, 2 desvios padrão acima e abaixo da média.
- Terra 99,7% das pontuações estão entre 700 e 1600, 3 desvios padrão acima e abaixo da média.


A regra empírica é uma forma rápida de obter uma visão geral dos seus dados e verificar se existem valores anómalos ou extremos que não sigam este padrão.
Se os dados de pequenas amostras não seguirem de perto este padrão, então outras distribuições como a distribuição t podem ser mais apropriadas. Uma vez identificada a distribuição da sua variável, você pode aplicar testes estatísticos apropriados.
Teorema do limite central
O teorema do limite central é a base de como as distribuições normais funcionam nas estatísticas.
Na pesquisa, para ter uma boa idéia de uma média populacional, idealmente você coletaria dados de múltiplas amostras aleatórias dentro da população. Uma distribuição por amostragem da média é a distribuição das médias destas diferentes amostras.
O teorema do limite central mostra o seguinte:
- Lei dos Grandes Números: medida que se aumenta o tamanho da amostra (ou o número de amostras), a média da amostra aproxima-se da média da população.
- Com várias amostras grandes, a distribuição da média por amostragem é normalmente distribuída, mesmo que a variável original não seja normalmente distribuída.
Testes estatísticos paramétricos normalmente assumem que as amostras vêm de populações normalmente distribuídas, mas o teorema do limite central significa que essa suposição não é necessária para atender quando se tem uma amostra grande o suficiente.
É possível usar testes paramétricos para amostras grandes de populações com qualquer tipo de distribuição, desde que outras suposições importantes sejam atendidas. Um tamanho de amostra de 30 ou mais é geralmente considerado grande.
Para amostras pequenas, a suposição de normalidade é importante, pois a distribuição da média por amostragem não é conhecida. Para obter resultados precisos, é necessário ter certeza de que a população é normalmente distribuída antes de usar testes paramétricos com amostras pequenas.
Fórmula da curva normal
Após ter a média e o desvio padrão de uma distribuição normal, você pode ajustar uma curva normal aos seus dados usando uma função de densidade de probabilidade.


Em uma função de densidade de probabilidade, a área sob a curva diz-lhe a probabilidade. A distribuição normal é uma distribuição de probabilidade, portanto a área total sob a curva é sempre 1 ou 100%.
A fórmula para a função de densidade de probabilidade normal parece bastante complicada. Mas para usá-la, você só precisa saber a média e o desvio padrão da população.
Para qualquer valor de x, você pode ligar a média e o desvio padrão na fórmula para encontrar a densidade de probabilidade da variável assumindo esse valor de x.
| Fórmula da Densidade de Probabilidade Normal | Explicação |
|---|---|
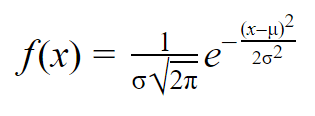 |
|
No seu gráfico da função de densidade de probabilidade, a probabilidade é a área sombreada sob a curva que fica à direita de onde seus resultados do SAT são iguais a 1380.


Você pode encontrar o valor de probabilidade deste resultado usando a distribuição normal padrão.
Qual é a distribuição normal padrão?
A distribuição normal padrão, também chamada de distribuição z, é uma distribuição normal especial onde a média é 0 e o desvio padrão é 1,
Tudo a distribuição normal é uma versão da distribuição normal padrão que foi esticada ou apertada e movida horizontalmente para a direita ou para a esquerda.


Apesar de observações individuais de distribuições normais serem referidas como x, elas são referidas como z na distribuição z. Cada distribuição normal pode ser convertida para a distribuição normal padrão transformando os valores individuais em z-scores.
Z-scores informam quantos desvios padrão se afastam da média de cada valor.


Você só precisa saber a média e o desvio padrão da sua distribuição para encontrar o z-score de um valor.
| Fórmula do z-score | Explicação |
|---|---|
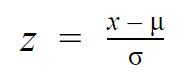 |
|
Convertemos as distribuições normais para a distribuição normal normal por várias razões:
- Para encontrar a probabilidade de observações em uma distribuição caindo acima ou abaixo de um determinado valor.
- Para encontrar a probabilidade de uma média amostral ser significativamente diferente de uma média populacional conhecida.
- Para comparar pontuações em diferentes distribuições com diferentes médias e desvios padrão.
Probabilidade usando a distribuição z
Cada z-score está associado a uma probabilidade, ou valor p, que lhe diz a probabilidade de ocorrência de valores abaixo desse z-score. Se você converter um valor individual em um z-score, você pode então encontrar a probabilidade de todos os valores até esse valor ocorrerem em uma distribuição normal.
A média da nossa distribuição é 1150, e o desvio padrão é 150. O z-score diz-lhe quantos desvios padrão está a 1380 da média.
| Fórmula | Cálculo |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
Para um z-score de 1,53, o p-valor é 0,937. Esta é a probabilidade da pontuação SAT ser 1380 ou menos (93,7%), e é a área sob a curva à esquerda da área sombreada.
>
>

Para encontrar a área sombreada, você tira 0.937 de 1, que é a área total sob a curva.
Probabilidade de x>1380 = 1 – 0,937 = 0,063
Isso significa que é provável que apenas 6,3% dos resultados do SAT na sua amostra excedam 1380,
Perguntas frequentes sobre distribuições normais
Em uma distribuição normal, os dados são distribuídos simetricamente, sem enviesamento. A maioria dos valores se agrupa em torno de uma região central, com valores caindo à medida que se afastam do centro.
As medidas de tendência central (média, modo e mediana) são exatamente as mesmas em uma distribuição normal.
A distribuição normal padrão, também chamada de distribuição z, é uma distribuição normal especial onde a média é 0 e o desvio padrão é 1,
Uma distribuição normal pode ser convertida na distribuição normal padrão transformando os valores individuais em z-scores. Numa distribuição z, as z-scores dizem-lhe quantos desvios padrão se afastam da média de cada valor.
A regra empírica, ou a regra 68-95-99.7, diz-lhe onde se encontra a maioria dos valores numa distribuição normal:
- A volta de 68% dos valores está dentro de 1 desvio padrão da média.
- A volta de 95% dos valores está dentro de 2 desvios padrão da média.
- Terra 99,7% dos valores estão dentro de 3 desvios padrão da média.
A regra empírica é uma forma rápida de obter uma visão geral dos seus dados e verificar se existem valores anómalos ou extremos que não seguem este padrão.
A distribuição t é uma forma de descrever um conjunto de observações onde a maioria das observações se aproxima da média, e o resto das observações formam as caudas de cada lado. É um tipo de distribuição normal usado para amostras de tamanho menor, onde a variância nos dados é desconhecida.
A distribuição t forma uma curva de sino quando plotada em um gráfico. Ela pode ser descrita matematicamente usando a média e o desvio padrão.

