Organic Chemistry II

Simples description

Vamos primeiro considerar a ligação pi em eteno de um ponto de vista simplificado da teoria MO (neste exemplo estaremos desconsiderando as ligações sigma na molécula, e pensando apenas na ligação π). Começamos com duas orbitais atômicas: uma orbital não-hibridizada de 2p de cada carbono. Cada uma contém um único elétron. Na teoria MO, os dois atômicos combinam-se matematicamente para formar dois orbitais moleculares pi, um orbital de ligação pi de baixa energia e outro orbital anti-ligação pi* de alta energia.

Orbitais moleculares para etileno (etileno)

No orbital pi de ligação, os dois lóbulos sombreados dos orbitais p interagem construtivamente um com o outro, assim como os dois lóbulos não sombreados (lembre-se, a escolha arbitrária de sombreamento representa sinais matemáticos (+) e (-) para a função de onda matemática descrevendo o orbital). Há aumento da densidade de elétrons entre os dois núcleos de carbono no orbital molecular – é uma interação de ligação.

No orbital pi* de maior energia antibondante, o lóbulo sombreado de um orbital p interage destrutivamente com o lóbulo não sombreado do segundo orbital p, levando a um nó entre os dois núcleos e repulsão geral entre os núcleos de carbono.

Again usando o princípio ‘building up’, nós colocamos os dois elétrons no orbital molecular pi de baixo consumo de energia, ligando o pi. O orbital pi* antiligação permanece vazio.

Mais detalhada descrição de MO do eteno

Teoria orbital molecular tem sido aplicada com muito sucesso a grandes sistemas conjugados, especialmente aqueles contendo cadeias de átomos de carbono com ligações simples e duplas alternadas. Uma aproximação introduzida por Hückel em 1931 considera apenas os elétrons p deslocalizados em um quadro de \pi -bonds. Esta é, na verdade, uma versão mais sofisticada de um modelo de elétrons livres. Para um curso introdutório de química orgânica não precisamos usar toda a matemática de Hückel, mas para aqueles que gostam de sondar mais profundamente, uma análise mais detalhada é dada aqui.

O hidrocarboneto mais simples a considerar que exibe \pi ligação é o eteno (etileno), que é composto por quatro átomos de hidrogênio e dois átomos de carbono. Experimentalmente, sabemos que os ângulos H-C-H e H-C-C-C no eteno são aproximadamente 120°. Este ângulo sugere que os átomos de carbono são sp2 hibridizados, o que significa que um orbital sp2 ocupado individualmente sobrepõe-se a um orbital s ocupado individualmente em cada H e um lóbulo sp2 ocupado individualmente no outro C. Assim, cada carbono forma um conjunto de três ligações \sigma: dois C-H (sp2 + s) e um C-C (sp2 + sp2) (parte (a) da Figura 13.1. abaixo).

Figure 13.1. (a) A estrutura de ligação σ é formada pela sobreposição de dois conjuntos de orbitais híbridos de carbono sp2 ocupados individualmente e quatro orbitais de hidrogênio 1s ocupados individualmente para formar ligações de pares de elétrons. Isto utiliza 10 dos 12 elétrons de valência para formar um total de cinco ligações σ (quatro ligações C-H e uma ligação C-C). (b) Um orbital de 2pz não-hibridizado, ocupado individualmente, permanece em cada átomo de carbono para formar uma ligação de carbono-carbono π. (Nota: por convenção, em moléculas planares o eixo perpendicular ao plano molecular é o eixo z.)

A aproximação Hückel é usada para determinar as energias e formas dos orbitais moleculares \pi em sistemas conjugados. Dentro da aproximação de Hückel, a ligação covalente nestes hidrocarbonetos pode ser separada em duas “estruturas” independentes: a estrutura de ligação \i1 e a estrutura de ligação \i1. As funções de onda usadas para descrever as orbitais de ligação em cada estrutura resultam de diferentes combinações de orbitais atómicos. O método limita-se a abordar os hidrocarbonetos conjugados e especificamente apenas as orbitais moleculares de electrões estão incluídas porque estas determinam as propriedades gerais destas moléculas; os electrões sigma são ignorados. Isto é referido como separabilidade sigma-pi e é justificado pela ortogonalidade dos orbitais sigma-pi nas moléculas planares. Por esta razão, o método de Hückel é limitado aos sistemas planares. A aproximação de Hückel assume que os elétrons das ligações de Hückel “sentem” um potencial eletrostático devido a toda a estrutura de ligação do sigma na molécula (ou seja, foca apenas na formação de ligações de Hückel, já que a estrutura de ligação do sigma já foi formada).

Ethene

Antes de considerar o tratamento de Hückel para o eteno, é benéfico rever o quadro geral de ligação da molécula. A colagem em eteno envolve a hibridação sp^2 dos orbitais atômicos 2s , 2p_x , e 2p_y em cada átomo de carbono; deixando os orbitais 2p_z intocados (Figura 13.2).

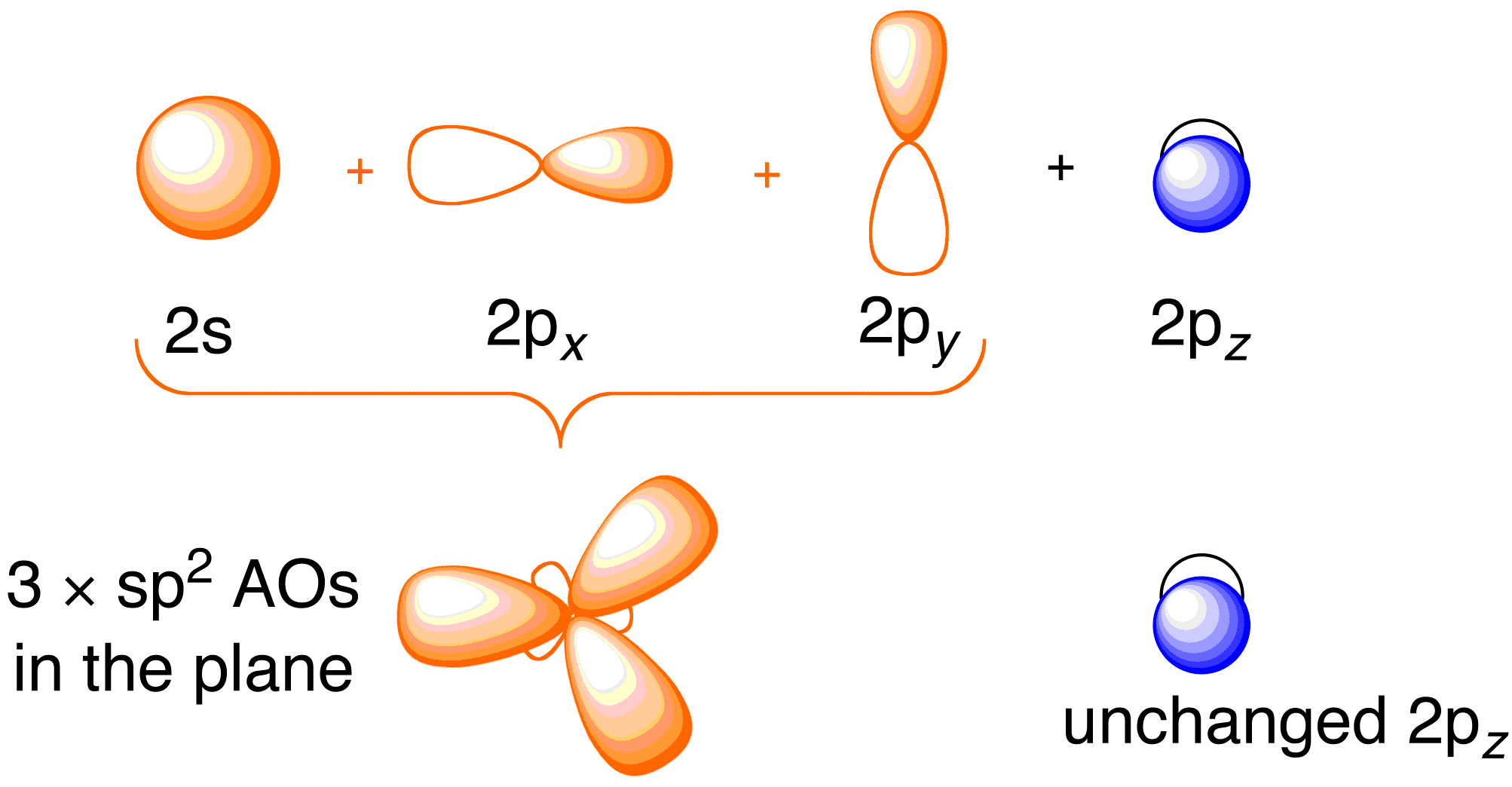
Figure 13.2. Hibridização dos orbitais atómicos de carbono para dar os orbitais híbridos sp^2 para ligação aos átomos de hidrogénio no eteno. Imagem usada com permissão da ChemTube (CC-SA-BY-NC; Nick Greeves).

O uso de orbitais híbridos na abordagem orbital molecular descrita aqui é apenas uma conveniência e não invoca a teoria da ligação de valência (diretamente). Uma descrição idêntica pode ser extraída usando exclusivamente orbitais atômicos sobre carbono, mas a interpretação das funções de onda resultantes é menos intuitiva. Por exemplo, o ith orbital molecular pode ser descrito via orbitais híbridos

\

ou via orbitais atômicos.

\\

onde \{a_i} e \c_i} são coeficientes da expansão. Qualquer um dos dois irá funcionar e ambos são abordagens idênticas uma vez que

>

onde {c_i} são coeficientes que descrevem o orbital hibridizado.

A ligação ocorre através da mistura dos electrões nos orbitais híbridos sp^2 sobre carbono e dos electrões nos orbitais atómicos 1s dos quatro átomos de hidrogénio (Figura 13.2. acima à esquerda) resultando na estrutura de ligação \sigma -bonding. A estrutura \pi -bonding framework resulta das orbitais 2p_z não-hibridizadas (Figura 13.2. acima, à direita). A independência dessas duas estruturas é demonstrada no diagrama orbital molecular resultante na Figura abaixo; a teoria de Hückel se preocupa apenas em descrever as orbitais moleculares e energias da estrutura de ligação \pi.

Figure 13.3: Orbitais moleculares demonstrando a separabilidade sigma-pi da estrutura de ligação \pi (azul) e das estruturas de ligação \pi (vermelho) de etileno.

O tratamento Hückel preocupa-se apenas em descrever as orbitais moleculares e as energias da estrutura de ligação da \pi.

Desde que a teoria de Hückel é uma consideração especial da teoria orbital molecular, os orbitais moleculares podem ser descritos como uma combinação linear dos orbitais atómicos de 2p_z com os seus correspondentes coeficientes de carbono:

Para a análise química quântica completa usando a equação de Schrödinger (não necessária para a classe de química orgânica), veja esta página de Libretexts.

Estes orbitais moleculares formam a estrutura de ligação π e como cada carbono contribui com um elétron para esta estrutura, apenas o orbital molecular mais baixo ( | \psi_1 \rangle ) é ocupado (Figura ) no estado de solo. A configuração eletrônica correspondente é então \pi_1^2 .

Figure 13.4: Representação esquemática da estrutura orbital molecular do \pi para etileno . Note-se que o orbital molecular antibloqueio tem um nó a mais do que o orbital molecular de ligação, como esperado, pois é mais alto em energia.

HOMO e LUMO são acrônimos para orbital molecular de maior ocupação e orbital molecular de menor desocupação, respectivamente, e são muitas vezes referidos como orbitais de fronteira. A diferença de energia entre o HOMO e o LUMO é chamada de lacuna HOMO-LUMO.

Os orbitais moleculares 3-D calculados \pi são mostrados na Figura 13.5.

Figure 13.5: Orbitais moleculares calculadas \pi para etileno . (esquerda) o orbital de ligação (ψ1) e (direita) o orbital de anti-ligação (ψ2).