Um triângulo com um ângulo recto é chamado de triângulo direito. O lado oposto ao ângulo reto é chamado de hipotenusa do triângulo. Os outros dois lados são chamados de perneiras. Os outros dois ângulos não têm nome especial, mas são sempre complementares. Vês porquê? A soma total dos ângulos de um triângulo é de 180 graus, e o ângulo reto é de 90 graus, então os outros dois devem somar 90 graus.
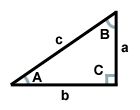
O triângulo acima tem o lado c como hipotenusa, os lados a e b como pernas, e o ângulo C como ângulo direito. Os ângulos A e B são complementares.
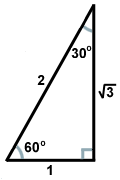
Existem dois tipos de triângulos rectos que qualquer matemático deve conhecer muito bem. Um é o triângulo direito formado quando uma altitude é desenhada a partir de um vértice de um triângulo equilátero, formando dois triângulos rectos congruentes. Os ângulos do triângulo serão de 30, 60 e 90 graus, dando ao triângulo o seu nome: triângulo 30-60-90. A proporção de comprimentos laterais em tais triângulos é sempre a mesma: se a perna oposta ao ângulo de 30 graus for de comprimento x, a perna oposta ao ângulo de 60 graus será de x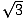
, e a hipotenusa transversal do ângulo direito será de 2x. Aqui está um triângulo de 30-60-90 representado abaixo.
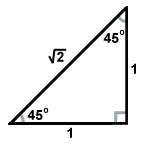
O outro triângulo direito comum resulta do par de triângulos criados quando uma diagonal divide um quadrado em dois triângulos. Cada um destes triângulos é congruente, e tem ângulos de medidas de 45, 45, e 90 graus. Se as pernas opostas aos ângulos de 45 graus são de comprimento x, a hipotenusa tem um comprimento de x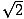
. Esta proporção é válida para todos os triângulos de 45-45-90 graus. Os triângulos 45-45-90 também são frequentemente chamados de triângulos isósceles direitos.
Uma última característica a notar é que as pernas de um triângulo direito também são altitudes do triângulo. Portanto, a área de um triângulo direito é metade do produto do comprimento de suas pernas.